分区算法
快排的基本动作是分区算法(3-way partition)。
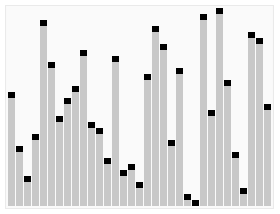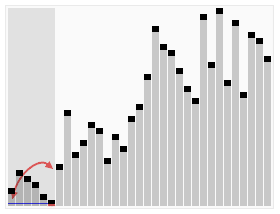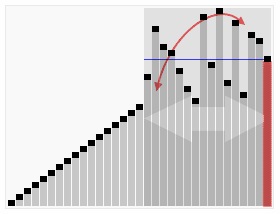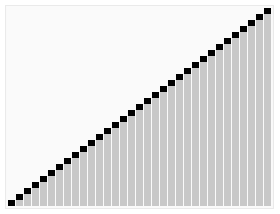
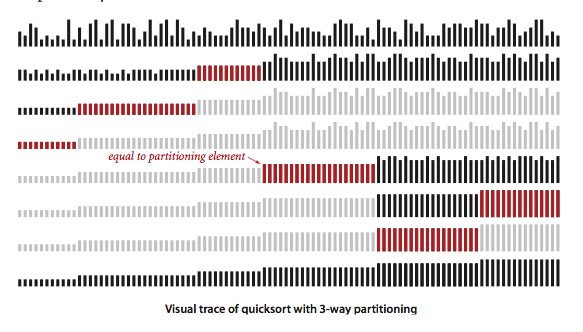
 如上图所示,分区算法的基本思想是:
如上图所示,分区算法的基本思想是:
不用精细地排序,选一个主元pivot,只是粗略地把一个数组划分成3部分:
< pivot,pivot,> pivot的元素。
分区算法代码
下面的Java代码是递归版的分区算法。
/**
* 将一个数组中指定区域的子数组分成三个部分:
* 1. 小于等于pivot元素的数(只要小于等于pivot元素就行,乱序)
* 2. 主元pivot
* 3. 大于pivot元素的数(只要大于pivot元素就行,乱序)
* 默认取最高位下标为pivot
* @param [array: 需要分区的数组]
* @param [low: 数组中需要分区的子数组的起始下标]
* @param [high: 数组中需要分区的子数组的结尾下标]
* @return [返回pivot元素的下标]
*/
public static int partition(int[] array, int low, int high) {
int bound = low-1;
int pivot = array[high];
for (int i = low; i< high; i++) {
if (array[i] <= pivot) {
bound++;
exchange(array,bound,i);
}
}
exchange(array,bound+1,high);
return bound+1;
}
/**
* [交换数组array中,第i个和第j个元素的值]
* @param [数组array]
* @param [下标i]
* @param [下标j]
*/
public static void exchange(int[] array, int i, int j) {
int temp = array[i];
array[i] = array[j];
array[j] = temp;
}
快排(Quick Sort)
分区以后,对子分区重复调用分区算法,就可以完成排序,这就是快排算法。用到了 分治 的思想。
快排代码
递归调用分区函数partition(),就是快排算法。
/**
* 复杂度为O(nlog(n))的快排。
* 主要就是递归调用数组划分函数: partition()
* @param [array: 排序的目标函数]
* @param [low: 排序区域的下界]
* @param [high: 排序区域的上界]
*/
public static void quickSort(int[] array, int low, int high) {
if (low < high) {
int pivot = partition(array,low,high);
quickSort(array,low,pivot-1);
quickSort(array,pivot+1,high);
}
}
快排动图
下图展示了快排是怎么给一个数组排序的,